
 |
Eager Space | Videos by Alpha | Videos by Date | All Video Text | Support | Community | About |
|---|


Description - links:
http://epizodsspace.airbase.ru/bibl/inostr-yazyki/tsiolkovskii/tsiolkovskii-nhedy-t2-1954.pdf
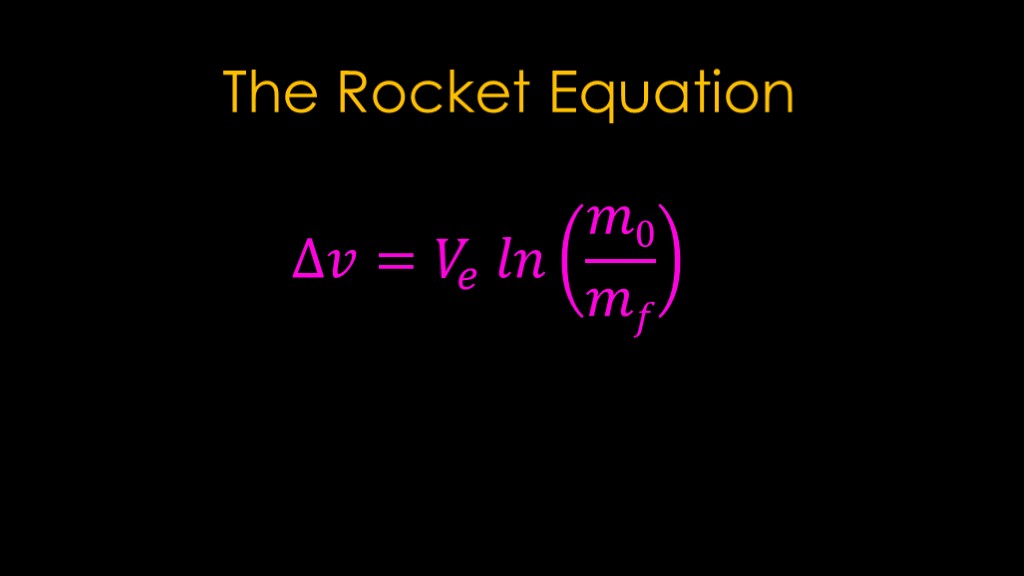
If you're interested in rockets and space, you may have encountered the rocket equation.
It looks complicated and it *is* rocket science, so it must be hard to understand....
But it's actually fairly simple, and you probably understand some of the basics already.
We'll need to take a bit of a side journey first...
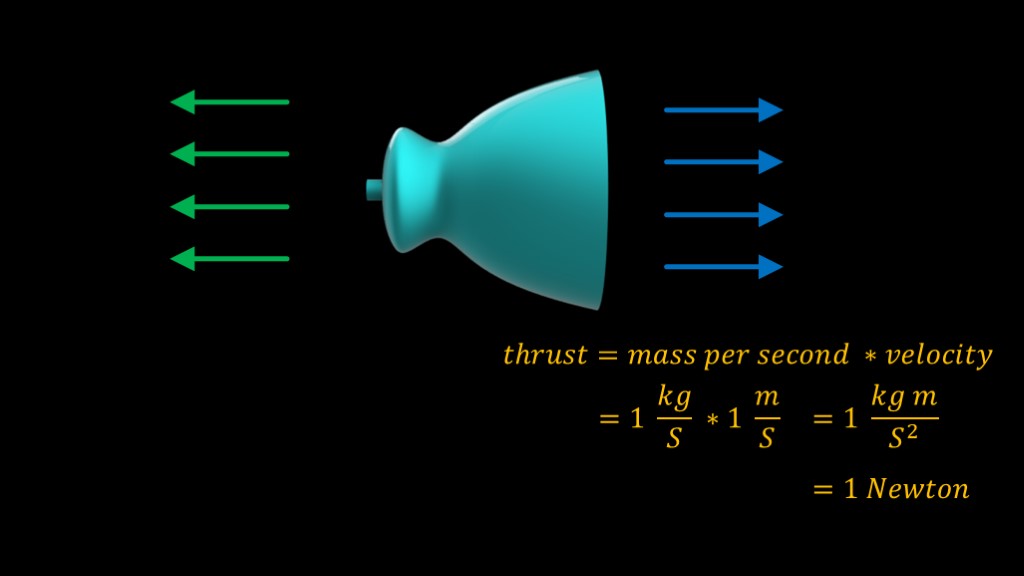
Rocket engines are reaction engines, which means they work by throwing mass out of the rocket nozzle, causing an opposite force pushing the rocket forward. We call that force "thrust".
It's pretty simple to define - it's equal to the amount of mass we are throwing out the engine every second multiplied by how quickly we are throwing that mass.
For example, we might be throwing 1 kilogram of mass out every second, and we might be throwing it out with a velocity of 1 meter per second. That gives us one kilogram meter per second squared.
That's a mouthful, so we write it as 1 newton. This is why thrust is measured in newtons, though you can also measure it in pounds of force if you prefer.
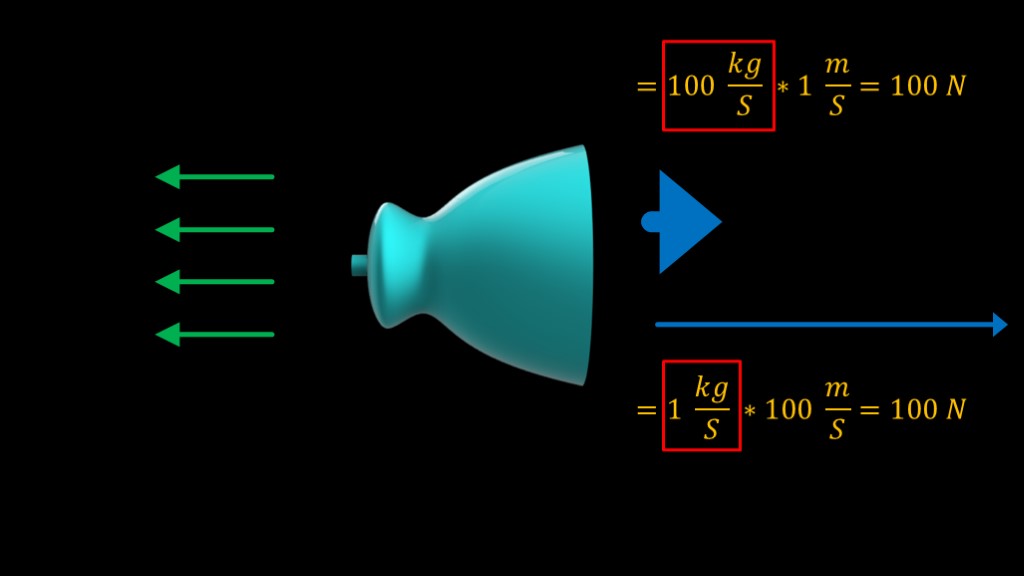
Since thrust depends on both the mass of the exhaust and how fast it is moving, we have a choice.
If we toss out 100 kilograms per second at a velocity of 1 meter per second, our thrust is 100 newtons
If we toss out 1 kilogram per second at a velocity of 100 meters per second, our thrust is also 100 newtons
The difference is that the first example burns 100 kilograms of propellant each second, and the second one burns 1 kilogram per second, so our propellant burn in the first case is 100 times the second case.
We therefore want the exhaust velocity of our rocket to be as high as possible.

How does this relate to actual rockets? It helps to look at an example.
Let's say we want to figure out how long it takes an rocket to burn through the propellant it carries.
The SpaceX Merlin 1D vacuum engine has a thrust of 981 kN. We know that thrust is equal to the mass per second times the velocity of that mass. In rocket terms, we would call that the mass flow rate times the exhaust velocity.
But all we know is the thrust, so how can we use this equation?
It actually turns out that we do know the exhaust velocity. Or - we know how to figure it out.

To explain I need to switch to a historical example
On the left, we have the rocketdyne f-1 engine used on the Saturn V, and on the right we have the NPO Energomash RD-170 engine used on the Energia.
If you ask the rocketdyne engineers what their exhaust velocity is, they say 8465 feet per second. Ask the NPO Energomash engineers, and they say 3031 meters per second.
We know that we prefer a higher exhaust velocity, but which one of these is better? Our units don't match, and neither group wants to switch to the other one's units. And converting could lead to mistakes.
What we need to do is get rid of the "feet" and "meters" in the measurements. Hmm... we know that the acceleration due to gravity uses those units, with 32.2 feet per second squared in imperial units and 9.81 meters per second squared in metric units.
Take the F-1 exhaust velocity and divide it by gravity, and we get 263 seconds. Do the same operation for the RD-170 and we get 309 seconds.
This is of course the specific impulse of the rocket engine, and since the RD-170 has a higher specific impulse, it has a higher exhaust velocity and is therefore more efficient when it comes how much mass it uses to generate a given amount of thrust. Specific impulse - often written as Isp - has the units of seconds, which we often ignore when writing the values.
If you are wondering why the RD-170 is so much more efficient, it is an advanced staged combustion design and the F-1 is less efficient gas-generator design. Note that the RD-170 is one engine with 4 separate nozzles.
What this means is that if you know the specific impulse of an engine, you can always figure out the exhaust velocity - just multiply it by gravity.
You'll find some discussions about the "seconds" in specific impulse meaning something like this: (read)
Yeah, I don't get it either, and all everybody cares about is exhaust velocity, so just remember that specific impulse is a simpler way to compare engines than exhaust velocity and you'll be fine.
If you want to know more about specific impulse, see my video "what's up with specific impulse?".

We can now return looking at the merlin 1d vacuum, and we have enough information to figure out the mass flow rate. After refactoring the equation to solve for mass flow rate, we plug in the values we know, and come up with 287 kilograms per second.
Before I learned this, I used to think that people who could figure out mass flow rates were doing some advanced work, but it turns out that it's really simple if you know the thrust and specific impulse.
BTW, if you know the mixture ratio for an engine, you can use that to figure out the mass flow rate of each propellant. If you care.

Now that we've talked about thrust, we can move towards the rocket equation.
We're going to look at the merlin 1d vacuum engine in a falcon 9 second stage, which has an empty mass of 3900 kilograms. We'll assume a payload of 10,000 kilograms. We just figured out that the mass flow rate for the engine is 287 kilograms per second.
If we put 1 second worth of fuel in the stage, that gives us a total mass of 14,187 kilograms. We know that acceleration = force divided by mass, so we take the force in newtons and divide it by total mass and we get 69.1 meters per second squared. For the last second of the burn, that's how much acceleration we will get.
Now we can look at the last 5 seconds of the burn. When there is 5 seconds of propellant left, our acceleration is 64 meters per second squared.
This isn't at all surprising - we would naturally expect the rocket to accelerate more slowly as we add more propellant mass.
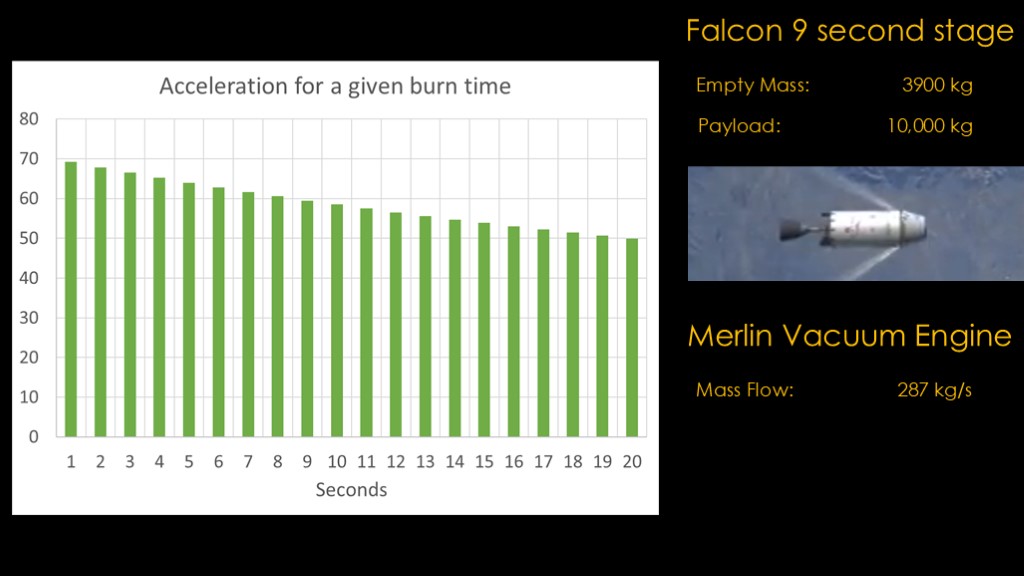
Here's a chart if we put 20 seconds of fuel in the stage. With 20 seconds of fuel in the stage, we only get 50 meters per second of acceleration.
Each additional second of propellant provides less benefit.
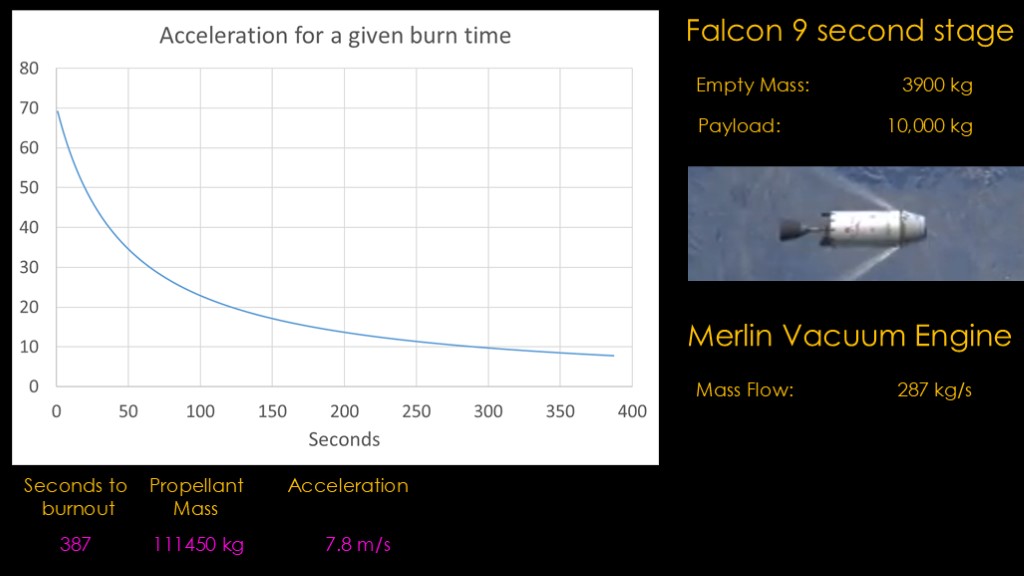
There's enough propellant in the stage to burn for 387 seconds, and if it's full it has over 111,000 kilograms of propellant, and the acceleration is only 7.8 meters per second squared.
Doing this for the whole burn gives us the following graph.
On the right side when the stage is full, it's very heavy and the thrust of the engine can only accelerate it slowly.
On the left side when the stage is nearly empty, it's very light and the thrust can accelerate it much faster.
It's a very simple concept.

If we want to know the total acceleration for this payload, we can add up the accelerations for each second.
That gives us 7460 meters per second. It's known as "delta v", where delta is the term used to mean "change" and v means velocity.
You might also see it written using the Greek letter delta - that's what the cool kids like to do.
It's not really very convenient, however, to add up all those numbers.
If you took calculus, I'm hoping at this point you're thinking "this looks familiar - I remember something about the area under a curve..."
And the answer is - of course - integration.

If you don't know or have forgotten how to do integration, don't worry. Wikipedia is happy to give you the details if you care about them.
The thing to remember is that the following formula is equivalent to adding up all the accelerations for each second because math.
It says that the total delta v is equal to the exhaust velocity multiplied by the natural log of the mass including fuel divided by the mass when all the fuel is gone. That part is often known as the mass ratio.
You will also see the exhaust velocity replaced with the specific impulse multiplied by the gravitational constant.
The rocket equation is really quite simple and the derivation is also simple - it's the sort of problem you might see in a physics class.

The rocket equation is generally credited to Konstantin Eduardovich Tsiolkovsky, from his 1903 work, exploration of the universe with reaction machines.
The derivation was, as I said, fairly straightforward, and had in fact been derived by British Mathematician William Moore in 1810 in his work, "on the motion of rockets both in nonresisting and resisting mediums". Tsiolkovsky gets the credit because he did a lot of other interesting work on rockets, including coming up with the concept of staging.
The equation would be re-derived by the American rocket researcher Robert Goddard in 1912, and finally, re-re-derived by German engineer Herman Oberth in 1920.

Let's return to our study of the Falcon 9 Second Stage...
We found that the full load of propellant gave us a delta v of around 7500 meters per second with a 10,000 kilogram payload.
But say that we need more delta-v. We somehow expand the stage so it carries twice as much propellant. How much delta v do we get out of the second 111,500 kilograms?
I'm hoping you aren't saying double. It is in fact only 1740 meters per second, for a total of 9240 meters per second.
If you keep going farther with this exercise, the third increment of 111,500 kilograms of propellant only nets 920 meters per second of additional delta v.
Also note that if you double or triple the propellant, you increase the size of your tanks and that reduces your mass ratio, so these numbers are optimistic.
The diminishing returns you get as you add more propellant is what people are referring to when they talk about "the tyranny of the rocket equation". It's really hard to push delta v numbers for a given stage higher.

Since we can't get more delta v by adding more propellant to our stage, we need a different solution...
We take our stage that can generate 7500 meters per second of delta v, and it becomes payload for our first stage, all 125,400 kilograms of it.
But that first stage only needs to generate about 1900 meters per second of delta v, and that's fairly easy even with the high payload mass. Easy enough that the first stage has enough delta v left over to land so that it can be reused.

We can compare this to a different rocket, the Atlas V with a centaur upper stage using the RL-10 engine.
The RL-10 burns hydrogen and oxygen and has a specific impulse of 465, which is great.
The final mass is the mass of the centaur stage - 2247 kilograms - plus the 10,000 kilogram payload
The initial mass is the final mass plus the amount of propellant the stage carries, which is 20,830 kilograms.
We have what we need to do the rocket equation. The delta v is 465 * 9.81 * the natural log of 33,077 kilograms divided by 12,247 kilograms). Do the calculation, and we get 4532 meters per second. That's only about 60% of the delta v that the Falcon 9 second stage produces? What is going on?
If we look at the Falcon 9 second stage numbers, it becomes clearer...
The Merlin vacuum specific impulse is only 348, or about 25% less than the 465 the RL-10 gets. The two stages are about the same dry weight, but the Merlin is burning RP-1, which is much, much denser than the hydrogen used by the RL-10 and the Falcon 9 second stage has slightly bigger tanks than the Centaur, so it packs in 111,500 kilograms of propellant versus the 20,830 kilograms the centaur has.
That gives the Falcon 9 second stage a mass ratio of 8.6 and the natural log of that is 2.1. The Centaur has a mass ratio of only 2.7, and the natural log of that is 1.0. The 25% specific impulse advantage of the RL-10 is overshadowed by the 210% advantage in mass ratio of the Falcon 9.
The same factor that gives you high specific impulse - light exhaust particles - means that you can fit less propellant in a given tank and therefore end up with a worse mass ratio.

Here's a graph that better illustrates the differences...
You can choose the delta v that you need and the specific impulse of your engine, and it will tell you what mass ratio you need.
We can add in the two examples, with the blue circle on the right showing the Falcon 9 second stage and the green circle on the left showing the Centaur. The Centaur has the more efficient engine, but the mass ratio it achieves is significantly inferior to the Falcon 9 and it only achieves 60% of the delta v of the Falcon 9 second stage.
It's important to note that part of this is an architectural choice - the Falcon 9 is designed to stage low so that the first stage can be reused and the Atlas V was designed to use the existing Centaur second stage and therefore needed a big beefy booster and solid rockets to give enough delta v to the centaur.
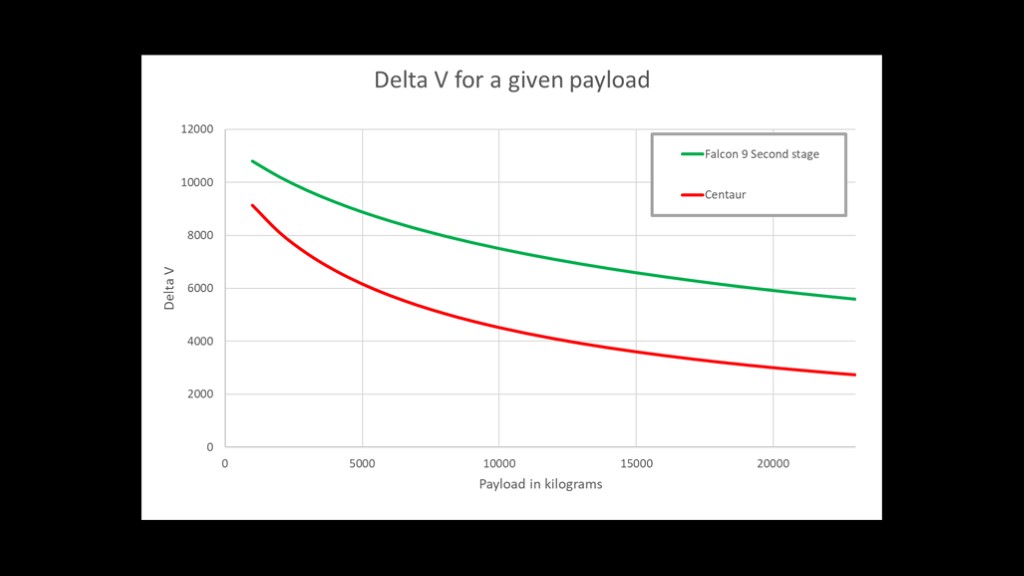
Here's another interesting graph, comparing the delta v that both stages can achieve with a given payload.
With a 1000 kilogram payload, the Falcon 9 second stage is only about 18% higher in delta v for a given payload, but as the payload mass goes up the centaur falls off quickly. Once we get up to 20,000 kilograms of payload, the Falcon 9 second stage is producing twice the delta v of the Centaur.
The centaur simply cannot overcome the low mass ratio despite having a specific impulse that is 30% better.

If you take one thing away from this video, let it be this.
If you are talking about specific impulse and you don't address the impact of the mass ratio of the whole vehicle, you simply do not know what you are talking about.
I see this all the time with discussions of nuclear thermal engines. Here's one that I liked:
"if the same mass fraction that was used for the chemical rocket engine case were used for the nuclear case, the travel time to Mars would be only 124 day".
It's a true statement, but tremendously misleading. Here are the numbers that we got from the centaur example. A comparable nuclear engine has a mass 2950 kilograms heavier than the RL-10, so our empty mass goes up to 15,196 kilograms. Since we fill the tanks only with hydrogen, the propellant mass goes way down, from 20,800 kilograms to 4,100 kilograms. The mass ratio goes from 2.7 down to 1.27.
The specific impulse is an impressive 900, but if you run the numbers, you get 2108 meters per second.
You need to consider the whole stage + payload when you look at specific impulse.

Here's another application of the rocket equation.
Let's look at an asteroid rendezvous mission. The internet says that the asteroid Davida is worth about $27 quintillion US dollars.
If you want to learn why that's not even close to true, see my video "asteroid mining buzzkill". But we'll pretend we want to do this mission and understand what sort of spacecraft we need to design.
511 Davida requires 6.17 km/s of delta v to get to, assuming we depart in July of 2035. Timing is very important when we are trying to journey beyond the moon; that is why missions to Mars launch every 26 months or so, when the delta v cost is the lowest.

It takes 6.17 kilometers per second to get from LEO to Davida. This in the same ballpark as what it takes to get a probe to Jupiter.
The usual way to do this is to use your launch vehicle to toss you wherever you want to go, but let's assume you want to start in LEO, because reasons.
We can refactor the rocket equation so that we can plug in the delta v we need and get back the mass ratio. E in the equation is the natural number e, which is about 2.7.
If we choose hypergolic propellants, they have a specific impulse of about 311. Plug that into the equation with the delta v we need, and the answer that we get is 7.6
That means we spend 12% of our mass on the spacecraft - the structure, the engines, the electronics, and whatever payload we are carrying - and 88% of our mass on propellant.
This illustrates why the usual method is to use the launch vehicle to provide the velocity to get away from earth.
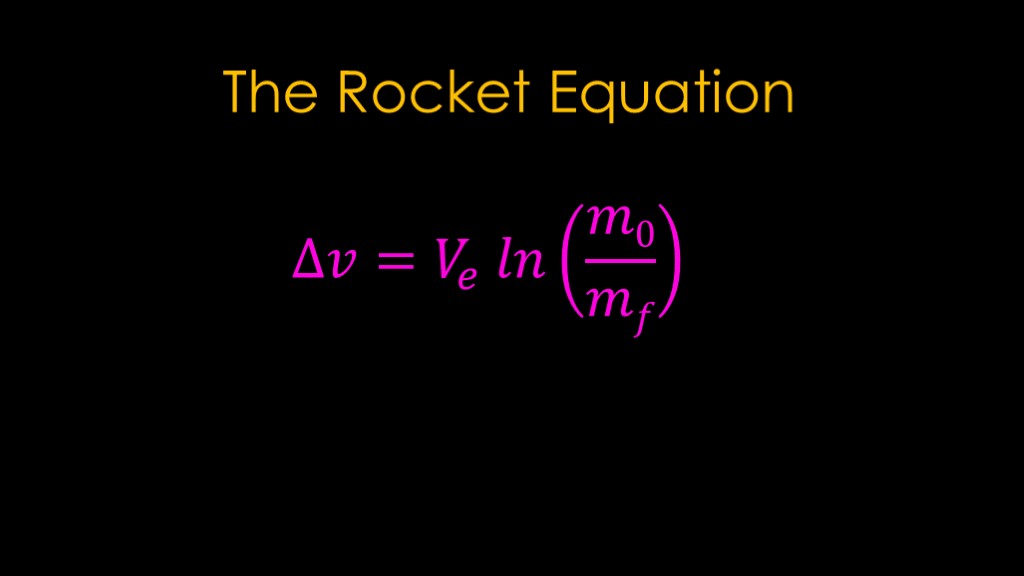
And that's all I have to say about the rocket equation.
Learn it. Know it. Live it.

If you enjoyed this video, please send me a model of the F-1 engine made out of peanut M&M's